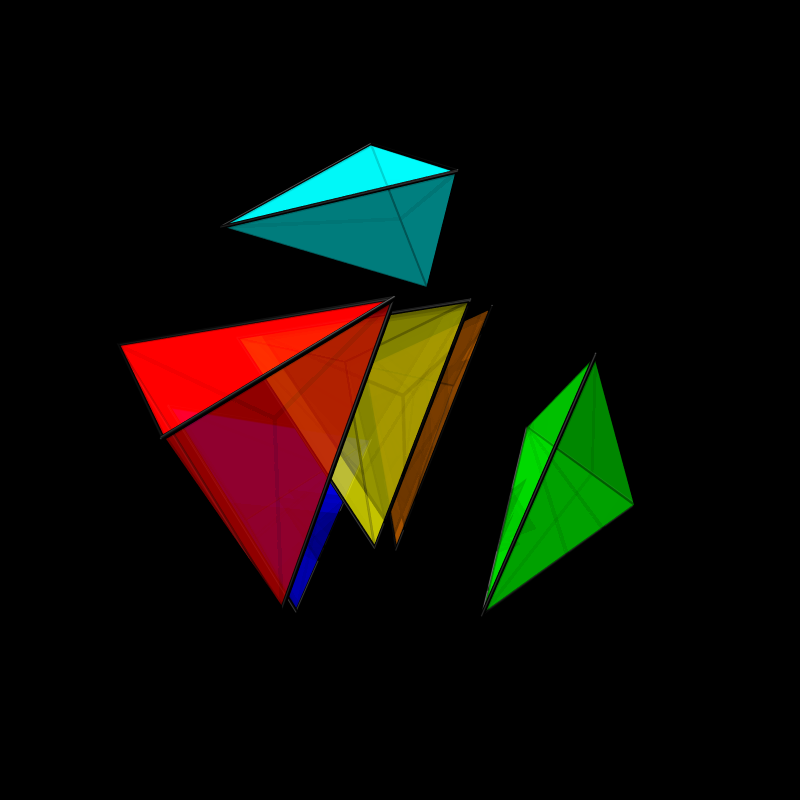
Cutting a cube into 6 tetrahedra
In the first lecture we have stacked steel balls onto each other and seen that for a tetrahedron the number of steel balls grows like g(n)= n(n+1)(n+2)/6. You have proven this in the worksheet. The algebra showed that g(n)-g(n-1) = n(n+1)/2 gives the triangular numbers. The triangular numbers in turn are the sum of the first n integers and the area of the base triangle slice of the tetrahedron. You have essentially verified with this computation that the volume of a tetrahedron is base area times height/3. The base area was n(n+1)/2 which is essentially length squared divided by 2, the area of a triangle of length n. If you imagine n to be large (each steel ball is an atom), we really compute area and volume and since g(n) is n3/6 plus terms n times smaller, we have verified using basic algebra only an important formula in geometry. Below is an animation which gives a geometric argument why the volume grows like that. The Egyptians or Greeks could derived it like this. They lacked the notion of function however, which deprived them from discovering calculus. Our first lecture on calculus could well have been a piece of calculus thousand years before it was discovered. An other Archimedes would have been needed. It could well have happened if not war would have destroyed these cultures. Or maybe Archimedes was just working on it, when he was killed drawing into the sand.

|
|