| Getting the notebook |
This summer, we pioneer a Mathematica lab with 3D printing. You have
templates, which can then be
printed and bought.
- A Mathematica demo file can be obtained here.
- The assignment for Summer 2012 is here!
Save this text file as "lab.nb" on your desktop and click on it.
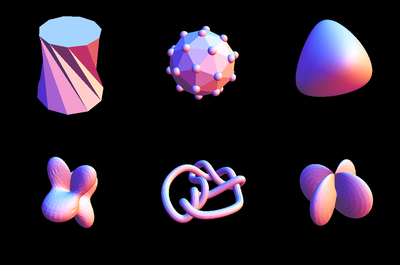
Here are the 6 example objects given in the assignment.

Project Hints
- Get inspired. If you use models you can find on the web like
here, acknowledge the models, you use.
More examples: something from the web
A = Import["http://www.georgehart.com/rp/sierpinski5-george-hart.stl"];
B = Import["http://www.georgehart.com/rp/Goldberg-8-3-george-hart.stl"];
Show[Graphics3D[{Scale[A[[1]],2],Translate[Scale[B[[1]],0.6],{1,1,3}]}],Boxed->False]
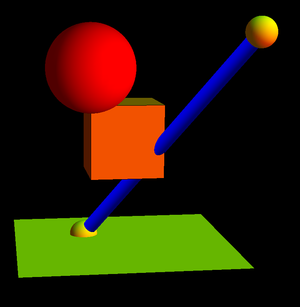
Here is maybe a bit simpler example: "Kung Fu":
A1 = {Blue, Cylinder[{{2, 1, 0}, {0, 3, 3}}, 0.1]};
A2 = {Red, Sphere[{2, 2, 2.5}, 0.6]};
A3 = {Orange, Cuboid[{1, 1, 1}, {2, 2, 2}]};
A4 = {Yellow, Sphere[{0, 3, 3}, 0.2]};
A4 = {Yellow, Sphere[{2, 1, 0}, 0.2]};
S = Show[Graphics3D[Scale[{A1, A2, A3, A4, A5}, 0.2]],
Axes -> True, PlotRange -> All, ViewPoint -> {0.51, 3.30, 0.494},
ViewVertical -> {0.11, 0.680, 0.76}]
 .
A list of Polyhedra can be obtained from .
A list of Polyhedra can be obtained from
PolyhedronData[]
Choose one and see it with
PolyhedronData["GyroelongatedPentagonalRotunda"]
- Check out the photos
of the printed models.
|
| Some basic commands:
|
| Plot[ x Sin[x],{x,-10,10}] | Graph function of one variable |
| Plot3D[ Sin[x y],{x,-2,2},{y,-2,2}] | Graph function of two variables |
| ParametricPlot[ {Cos[3 t],Sin[5 t]} ,{t,0,2Pi}] | Plot planar curve |
| ParametricPlot3D[{Cos[t],Sin[t],t} ,{t,0,4Pi},AspectRatio->1] | Plot space curve |
| ParametricPlot3D[{Cos[t] Sin[s],Sin[t] Sin[s],Cos[s]},{t,0,2Pi},{s,0,Pi}] | Parametric Surface |
| SphericalPlot3D[(2+Sin[2 t] Sin[3 s]),{t,0,Pi},{s,0,2 Pi}] | Spherical Plot |
| RevolutionPlot3D[{2 + Cos[t], t}, {t,0,2 Pi}] | Revolution Plot |
| ContourPlot[Sin[x y],{x,-2,2},{y,-2,2} ] | Contour lines (traces) |
| ContourPlot3D[x^2+2y^2-z^2,{x,-2,2},{y,-2,2},{z,-2,2}] | Implicit surface |
VectorPlot[{x-y,x+y},{x,-3,3},{y,-3,3}] | Vectorfield plot |
VectorPlot3D[{x-y,x+y,z},{x,-3,3},{y,-3,3},{z,0,1}] | Vectorfield plot 3D |
Integrate[x Sin[x], x] | Integrate symbolically |
| Integrate[x y^2-z,{x,0,2},{y,0,x},{z,0,y}] | 3D Integral |
| NIntegrate[Exp[-x^2],{x,0,10}] | Integrate numerically |
| D[ Cos^5[x],x ] | Differentiate symbolically |
| Series[Exp[x],{x,0,3} ] | Taylor series |
| DSolve[ x''[t]==-x[t],x,t ] | Solution to ODE |
| DSolve[{D[u[x,t],t]==D[u[x,t],x],u[x,0]==Sin[x]},u[x,t],{x,t}] | Solution to PDE |
Classify extrema:
ClassifyCriticalPoints[f_,{x_,y_}]:=Module[{X,P,H,g,d,S}, X={x,y};
P=Sort[Solve[Thread[D[f,#] & /@ X==0],X]]; H=Outer[D[f,#1,#2]&,X,X];g=H[[1,1]];d=Det[H];
S[d_,g_]:=If[d<0,"saddle",If[g>0,"minimum","maximum"]];
TableForm[{x,y,d,g,S[d,g],f} /.P,TableHeadings->{None,{x,y,"D","f_xx","Type","f"}}]]
ClassifyCriticalPoints[4 x y - x^3 y - x y^3,{x,y}]
Solve a Lagrange problem:
F[x_,y_]:=2x^2+4 x y; G[x_,y_]:=x^2 y;
Solve[{D[F[x,y],x]==L*D[G[x,y],x],D[F[x,y],y]==L*D[G[x,y],y],G[x,y]==1},{x,y,L}]
Check that a function solves a PDE:
f[t_,x_]:=(x/t)*Sqrt[1/t]*Exp[-x^2/(4 t)]/(1+ Sqrt[1/t] Exp[-x^2/(4 t)]);
D[f[t,x],t]+f[t,x]*D[f[t,x],x]-D[f[t,x],{x,2}]
Simplify[%] Chop[%]
|


