HCRP project 2009
geodesics on surface of revolution
Geodesics on surface of revolution
Office: SciCtr 434
Email: knill@math.harvard.edu
 |
 |
||||||
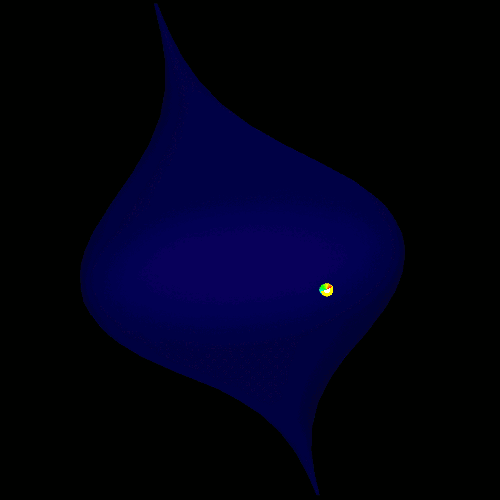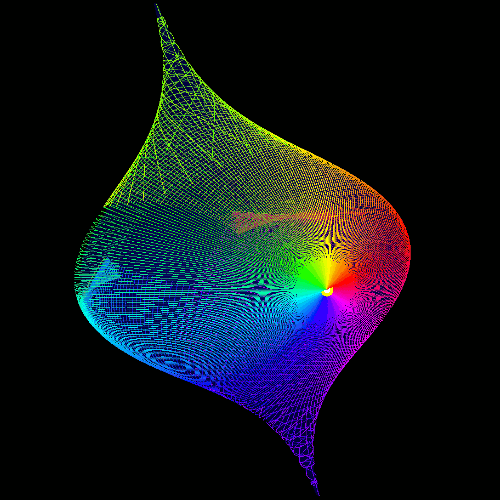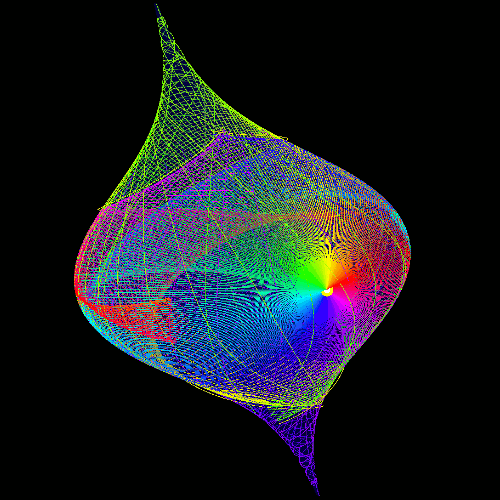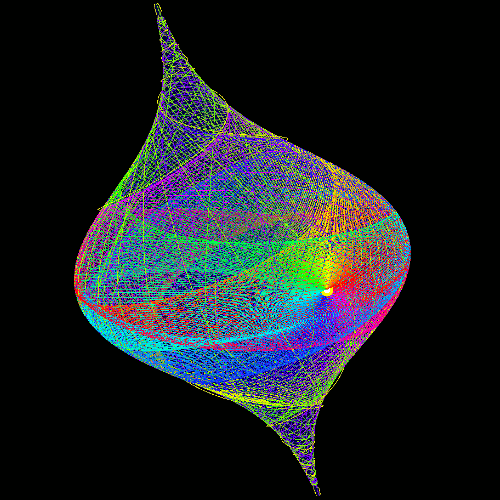| Animation of the geodesic evolution on the surface given in cylindrical coordinates as r=exp(-z2). | |||||||
 |
 |
| Motion of the caustic in dependence on the initial point | |
 |
 |
| Primary caustic computation on a surface of revolution r = exp(-z^2). There are directions, in which the geodesic winds around the torus several times before the Jacobi field reaches a zero. For these pictures, 10'000 geodesics have been started from one point and integrated until time 10. Always the first point was marked, where the Jacobi field is zero. | |