Numerics of Geodesics Computation

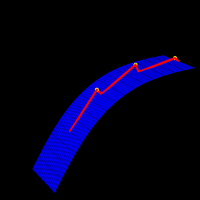There is a fast method to compute geodesics on surfaces embedded in space: do a free evolution in space with a strong force gluing the particle to the surface. Illustrations done for the book "Moser: Selected topics in the calculus of variations" (appeared in 2003) have used this method. Example [ JPG ]. Even with primitive Euler steps, the evolution is assured to stay on the unit tangent bundle. This handout (PDF) from 2005 explains this method briefly. This method has also been used by Sinclair in this article. This method is justified by the fact that the differential equations of a geodesic on a hyperplane are x'' = - n (D_j n_k) x_k x_j = - (D_x' n) n. These equations tell that the 'force' gluing the geodesics onto the hypersurface is normal towards the surface and has as its magnitude the covariant derivative of n in the velocity direction x'. This is the infinitesimal description of "moving straight" while being "pulled back normally" to the surface just enough to stay on the surface.

For our Spring 2009 project, we computed caustics directly by integrated the differential equations

    g''(t)^k  + G_ij^k gⁱ'(t) g^j'(t)  = 0 
    f''(t) + K(g(t)) f(t) = 0

The code is very general and can handle any parametrized surface r(u,v) = (x(u,v),y(u,v),z(u,v)). Integrating the differential equations numerically with built in NDSolve method in the computer algebra system was not good enough for us. Here are the reasons:

First of all, we need to note, each times, when f(t) has become zero to get the caustic.
Second, we need to assure we stay on the unit tangent bundle. The velocity of the particle stays constant.
Third, we occasionally need to work with different charts of the manifold. On the ellipsoid for example, the spherical parametrization is bad near the poles. On a torus, we have identifications which need to be observed.

In the case of the ellipsoid r(u,v) = (a cos(u) sin(v),b sin(u) sin(v),cos(v) ) for example, we have in spherical coordinates the differential equations

u'' = -(2*a^2*b^2*u'*v'*cos(u)^4*cos(v)^2*cot(v) - 
      ((a^2 - b^2)*(-u'^2 - 2*v'^2 + u'^2*cos(2*v))*sin(2*u))/4 + 
      b^2*u'*v'*cos(u)^2*(4*a^2*cos(v)^2*cot(v)*sin(u)^2 + sin(2*v)) + 
      a^2*u'*v'*sin(u)^2*(2*b^2*cos(v)^2*cot(v)*sin(u)^2 + sin(2*v)))/
     (a^2*b^2*cos(u)^4*cos(v)^2 + b^2*cos(u)^2*(2*a^2*cos(v)^2*sin(u)^2 + 
        sin(v)^2) + a^2*sin(u)^2*(b^2*cos(v)^2*sin(u)^2 + sin(v)^2));
 
v''= -(-2*(-(b^2*v'^2) + a^2*(-v'^2 + 2*b^2*(u'^2 + v'^2)) + 
       (a^2 - b^2)*v'^2*cos(2*u))*sin(2*v))/(2*a^2 + 2*b^2 + 
      4*a^2*b^2 - 2*(a^2 - b^2)*cos(2*u) + (a^2 - b^2)*cos(2*(u - v)) - 
      2*a^2*cos(2*v) - 2*b^2*cos(2*v) + 4*a^2*b^2*cos(2*v) + 
      a^2*cos(2*(u + v)) - b^2*cos(2*(u + v)));

f''= - f (a^2*b^2)/(a^2*b^2*cos(u)^4*cos(v)^2 + b^2*cos(u)^2*
        (2*a^2*cos(v)^2*sin(u)^2 + sin(v)^2) + a^2*sin(u)^2*
        (b^2*cos(v)^2*sin(u)^2 + sin(v)^2))^2

When dealing with a single case, optimizations could be done like storing terms like cos(2*(u-v)) before so that the cos does not have to be computed several times. In general, we have much more complicated formulas: here is an example of an asymetrically deformed torus:

r(u,v)={(2+(1+R cos(u)) cos(v)) cos(u),(2+(1+R cos(u)) cos(v))sin(u),sin(v)};

u'' = (-8 (-(R (-up^2 + vp^2 + R vp^2 cos(u)) cos(v)^4 sin(u)) +
       2 up cos(v)^3 (R up sin(u) + vp (1 + R^2 + 2 R cos(u)) sin(v)) +
       (up (1 + R cos(u))^2 cos(v) sin(v)^2 (8 R up sin(u) +
          2 vp (2 + R^2 + 4 R cos(u) + R^2 cos(u)^2) sin(v) -
          2 R^2 vp sin(u)^2 sin(v)))/2 + cos(v)^2 sin(v) 
        (4 up vp - R vp^2 sin(u) sin(v) + 6 R^2 up^2 cos(u)^3 sin(u) sin(v) +
         6 R^3 up^2 cos(u)^4 sin(u) sin(v) + 2 R^4 up^2 cos(u)^5 sin(u) 
          sin(v) + 2 R up^2 sin(u)^3 sin(v) + 2 R up^2 cos(u)^2 sin(u) 
          (1 + 3 R^2 sin(u)^2) sin(v) + R cos(u) (4 up vp -
           R vp^2 sin(u) sin(v) + 6 R up^2 sin(u)^3 sin(v))) +
       (up (64 vp cos(u)^2 sin(v)^3 + 192 R vp cos(u)^3 sin(v)^3 +
          192 R^2 vp cos(u)^4 sin(v)^3 + 64 R^3 vp cos(u)^5 sin(v)^3 +
          64 vp sin(u)^2 sin(v)^3 + 96 R vp sin(u) sin(2 u) sin(v)^3 +
          R^2 sin(2 u)^2 (16 vp (3 + R cos(u)) sin(v)^3 + R^2 up sin(2 u) 
             sin(2 v)^2)))/16))/(32 (1 + R cos(u)) cos(v)^3 +
      8 (1 + R^2 + 2 R cos(u)) cos(v)^4 + 32 cos(u)^2 sin(v)^2 +
      64 R cos(u)^3 sin(v)^2 + 32 R^2 cos(u)^4 sin(v)^2 +
      32 (1 + R cos(u))^3 cos(v) sin(v)^2 + 32 sin(u)^2 sin(v)^2 +
      16 R cos(u) (5 + cos(2 v)) sin(u)^2 sin(v)^2 +
      8 R^2 sin(2 u)^2 sin(v)^2 + 8 cos(v)^2 (4 + cos(u)^2 sin(v)^2 +
        4 R cos(u)^3 sin(v)^2 + 4 R^3 cos(u)^5 sin(v)^2 +
        R^4 cos(u)^6 sin(v)^2 + R^2 cos(u)^4 (6 + R^2 sin(u)^2) sin(v)^2) +
      2 sin(u)^2 sin(2 v)^2 + 3 R^2 sin(2 u)^2 sin(2 v)^2 +
      R^3 csc(u) sin(2 u)^3 sin(2 v)^2);

v'' = (8 sin(v) (R^4 (2 up^2 + vp^2) cos(u)^6 cos(v)^3 +
       R^3 cos(u)^5 cos(v)^2 (10 up^2 + 4 vp^2 + (7 up^2 + 4 vp^2) cos(v)) +
       cos(v)^3 (-vp^2 + (up^2 + vp^2 - R^2 vp^2) sin(u)^2 +
         2 R^2 up^2 sin(u)^4) + cos(v)^2 (-4 vp^2 + (6 up^2 + 4 vp^2) 
          sin(u)^2 + 4 R^2 up^2 sin(u)^4) + 8 up sin(u)^2 
        (up - R vp sin(u) sin(v)) + 4 cos(v) (-vp^2 + (3 up^2 + vp^2) 
          sin(u)^2 - R up vp sin(u)^3 sin(v)) +
       R cos(u)^3 (2 cos(v)^2 (11 up^2 + 6 vp^2 + R^2 (7 up^2 + 2 vp^2) 
            sin(u)^2) + cos(v)^3 (5 up^2 + 4 vp^2 + R^2 (11 up^2 + 4 vp^2) 
            sin(u)^2) + 8 up (up - R vp sin(u) sin(v)) +
         4 cos(v) (7 up^2 + 2 vp^2 - 2 R up vp sin(u) sin(v))) +
       R cos(u) (2 cos(v)^2 (-2 vp^2 + (11 up^2 + 6 vp^2) sin(u)^2 +
           2 R^2 up^2 sin(u)^4) + cos(v)^3 (-2 vp^2 + (5 up^2 + 4 vp^2) 
            sin(u)^2 + 4 R^2 up^2 sin(u)^4) + 8 up sin(u)^2 
          (up - R vp sin(u) sin(v)) + 4 cos(v) sin(u)^2 (7 up^2 + 2 vp^2 -
           2 R up vp sin(u) sin(v))) + R^2 cos(u)^4 cos(v) 
        (2 (13 up^2 + 6 vp^2) cos(v) + cos(v)^2 (9 up^2 + 6 vp^2 +
           R^2 (4 up^2 + vp^2) sin(u)^2) + 4 (4 up^2 + vp^2 -
           R up vp sin(u) sin(v))) + cos(u)^2 
        (2 cos(v)^2 (3 up^2 + 2 vp^2 + 3 R^2 (5 up^2 + 2 vp^2) sin(u)^2) +
         cos(v)^3 (up^2 + vp^2 - R^2 vp^2 + R^2 (11 up^2 + 6 vp^2) sin(u)^2 +
           2 R^4 up^2 sin(u)^4) + 8 up (up - R vp sin(u) sin(v)) +
         4 cos(v) (3 up^2 + vp^2 + R^2 (4 up^2 + vp^2) sin(u)^2 -
           R up vp sin(u) sin(v) - R^3 up vp sin(u)^3 sin(v)))))/
     (32 (1 + R cos(u)) cos(v)^3 + 8 (1 + R^2 + 2 R cos(u)) cos(v)^4 +
      32 cos(u)^2 sin(v)^2 + 64 R cos(u)^3 sin(v)^2 +
      32 R^2 cos(u)^4 sin(v)^2 + 32 (1 + R cos(u))^3 cos(v) sin(v)^2 +
      32 sin(u)^2 sin(v)^2 + 16 R cos(u) (5 + cos(2 v)) sin(u)^2 sin(v)^2 +
      8 R^2 sin(2 u)^2 sin(v)^2 + 8 cos(v)^2 (4 + cos(u)^2 sin(v)^2 +
        4 R cos(u)^3 sin(v)^2 + 4 R^3 cos(u)^5 sin(v)^2 +
        R^4 cos(u)^6 sin(v)^2 + R^2 cos(u)^4 (6 + R^2 sin(u)^2) sin(v)^2) +
      2 sin(u)^2 sin(2 v)^2 + 3 R^2 sin(2 u)^2 sin(2 v)^2 +
      R^3 csc(u) sin(2 u)^3 sin(2 v)^2);

f'' = -f (2 cos(v) (352 + 240 R^2 + 8 R (76 + 17 R^2) cos(u) +
       176 R^2 cos(2 u) + 24 R^3 cos(3 u) + 20 R cos(u - 3 v) +
       25 R^3 cos(u - 3 v) + 6 R^2 cos(2 u - 3 v) + 4 R^4 cos(2 u - 3 v) +
       176 R cos(u - 2 v) + 68 R^3 cos(u - 2 v) + 12 R^3 cos(3 u - 2 v) +
       508 R cos(u - v) + 75 R^3 cos(u - v) + 88 R^2 cos(2 (u - v)) +
       3 R^3 cos(3 (u - v)) + 178 R^2 cos(2 u - v) + 12 R^4 cos(2 u - v) +
       9 R^3 cos(3 u - v) + 408 cos(v) + 372 R^2 cos(v) + 24 R^4 cos(v) +
       96 cos(2 v) + 240 R^2 cos(2 v) + 8 cos(3 v) + 60 R^2 cos(3 v) +
       8 R^4 cos(3 v) + 508 R cos(u + v) + 75 R^3 cos(u + v) +
       88 R^2 cos(2 (u + v)) + 3 R^3 cos(3 (u + v)) + 178 R^2 cos(2 u + v) +
       12 R^4 cos(2 u + v) + 9 R^3 cos(3 u + v) + 176 R cos(u + 2 v) +
       68 R^3 cos(u + 2 v) + 12 R^3 cos(3 u + 2 v) + 20 R cos(u + 3 v) +
       25 R^3 cos(u + 3 v) + 6 R^2 cos(2 u + 3 v) + 4 R^4 cos(2 u + 3 v)))/
     (32 (1 + R cos(u)) cos(v)^3 + 8 (1 + R^2 + 2 R cos(u)) cos(v)^4 +
       32 cos(u)^2 sin(v)^2 + 64 R cos(u)^3 sin(v)^2 +
       32 R^2 cos(u)^4 sin(v)^2 + 32 (1 + R cos(u))^3 cos(v) sin(v)^2 +
       32 sin(u)^2 sin(v)^2 + 16 R cos(u) (5 + cos(2 v)) sin(u)^2 sin(v)^2 +
       8 R^2 sin(2 u)^2 sin(v)^2 + 8 cos(v)^2 (4 + cos(u)^2 sin(v)^2 +
         4 R cos(u)^3 sin(v)^2 + 4 R^3 cos(u)^5 sin(v)^2 +
         R^4 cos(u)^6 sin(v)^2 + R^2 cos(u)^4 (6 + R^2 sin(u)^2) sin(v)^2) +
       2 sin(u)^2 sin(2 v)^2 + 3 R^2 sin(2 u)^2 sin(2 v)^2 +
       R^3 csc(u) sin(2 u)^3 sin(2 v)^2)^2;